[0314 복습] 평균추정과 신뢰구간, 중심극한정리, 이변량분석_범주형(교차표 crosstab, mosaic plot, 카이제곱 검정)
CH07 평균 추정과 신뢰구간
분산(Var, Variance), 표준편차(SD, Standard Deviation)
한 집단의 대푯값으로 평균을 계산했을 때, 값들이 평균으로부터 얼마나 벗어나 있는지를 나타내는 값(이탈도, deviation)
표본의 목적 → 모집단 추정 / 표본평균: 모평균에 대한 추정치
표준오차
추정치에는 오차가 존재하는데 이 오차를 표준오차
표준오차: s / √n (s = 샘플의 표준 편차, n = 데이터 건수)
**표본집합을 100개 추출하고, 그 표본의 평균의 분포를 보면 정규분포 형태로 나타난다!
→ 이 정규분포의 표준편차를 표준오차로 볼 수 있다!
why? 모평균과 표본평균의 차이 = 오차 → 표본평균의 분포의 표준편차 = 표준오차
95% 신뢰구간
표준오차를 바탕으로 95% 확률 구간 계산 가능
95% 신뢰구간: 표본평균 - 1.96 * SE(표준오차) ~ 표본평균 + 1.96 * SE
- 신뢰구간 안에 모평균이 포함될 확률이 95%이다!
중심극한정리
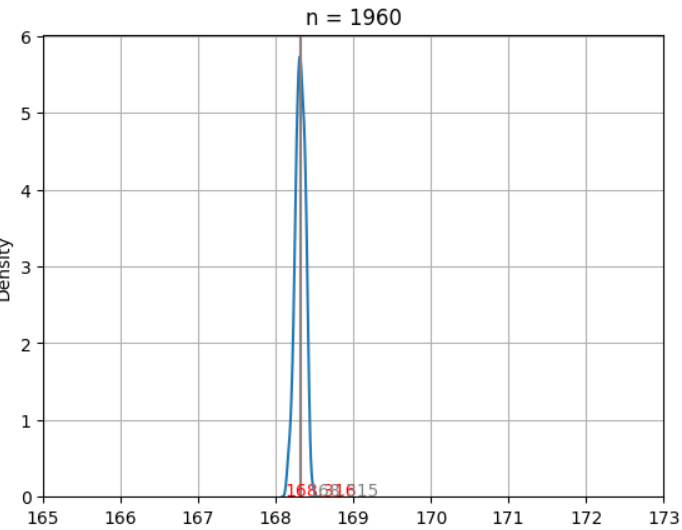
표본이 클수록 정규분포 모양이 중심에 가까워지는 좁은 형태가 된다!
→ 이 분포(표본평균들의 분포)의 평균: 모평균에 매우 가깝다!
CH09 이변량분석_범주 → 범주
교차표(crosstab)
범주 vs 범주를 비교하고 분석하기 위해서 먼저 교차표 제작 / 범주와 범주의 값을 크로스해서 값을 데이터프레임 형태로
- nomalize = 'columns' 옵션을 주면 열 기준 합이 1(100%)이 되도록 크로스탭 작성
- nomalize = 'index' 옵션을 주면 행 기준 합이 1(100%)이 되도록 크로스탭 작성
- nomalize = 'all' 옵션을 주면 전체 기준 합이 1(100%)이 되도록 크로스탭 작성
#범주형1의 값에 따른 범주형2의 비율 계산
pd.crosstab(df['범주형1'], df['범주형2'], nomalize='columns')
시각화: 모자이크 플롯(mosaic)
범주별 양과 비율을 그래프로 알아서 나타내 줌!
# 객실등급별 생존여부를 mosaic plot으로 그려 봅시다.
mosaic(titanic, ['Pclass','Survived'])
plt.axhline(1- titanic['Survived'].mean(), color = 'r') # 전체평균 선 표시
plt.show()
- 빨간 선은 전체 평균을 의미!
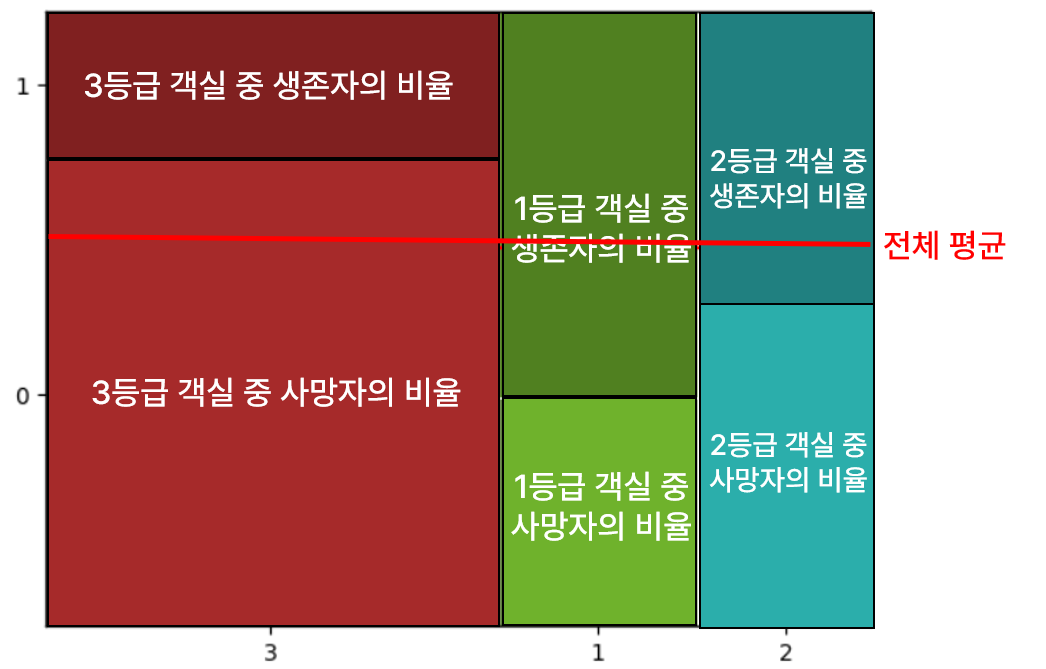
** 두 범주형 변수가 아무런 상관이 없다면, 범주 별 비율의 차이가 전체평균과 차이가 전혀 없는 상태가 됨!
** 각 등급별로 전체 평균 비율과 차이가 많이 난다면 영향을 강하게 미치는 것!
참고) Stacked Bar
# 비율만 보이고 이 순서대로 코드를 작성해야 함 ********************
temp = pd.crosstab(titanic['Pclass'], titanic['Survived'], normalize = 'index')
print(temp)
temp.plot.bar(stacked=True)
plt.axhline(1-titanic['Survived'].mean(), color = 'r')
plt.show()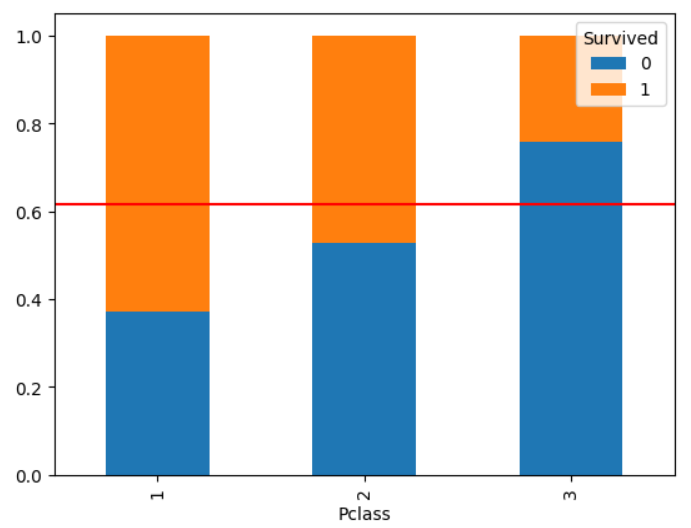
수치화: 카이제곱 검정
- 카이제곱 검정: 범주형 변수들 사이에 어떤 관계가 있는지 수치화하는 방법
♣ 기대빈도: 범주형 변수들이 아무런 관련이 없을 때 나올 수 있는 빈도수!
♣ 실제 데이터: 관측된 값들!
기대빈도를 기준으로 기대빈도와 실제 데이터 사이의 차이에 따라서 범주 → 범주의 관계를 판단!
** 카이제곱 통계량은 클수록 기대빈도로부터 실제 값의 차이가 크다는 의미!
** 범주의 수가 늘어날수록 값은 커짐, 자유도의 약 2배보다 크면, 차이가 있다고 봄!
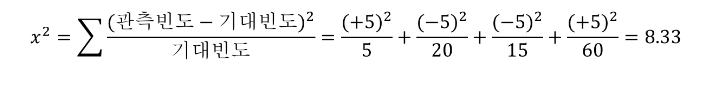
- 자유도: 범주의 수 -1
- 카이제곱검정에서의 자유도: x 변수의 자유도 * y 변수의 자유도 > 2보다 카이제곱 통계량이 크면, 차이가 있다고 볼 수 있음!
# 1) 먼저 교차표 집계- normalize 하면 안 됨, 그대로 count하도록 해야 함
table = pd.crosstab(df['x 변수'], df['y 변수'])
print(table)
print('-' * 50)
# 2) 카이제곱검정
spst.chi2_contingency(table)
# statistic = 카이제곱 통계량, expected_Freq(기대 빈도)