[0401 복습] 머신러닝 마무리_로지스틱 회귀분석, K-Fold Cross Validation(k-분할 교차 검증), 성능 예측, 하이퍼파라미터 튜닝, Random Search, Grid Search

KT 에이블스쿨 복습

[0401 복습] 머신러닝 마무리_로지스틱 회귀분석, K-Fold Cross Validation(k-분할 교차 검증), 성능 예측, 하이퍼파라미터 튜닝, Random Search, Grid Search

리니끄적 2024. 4. 1. 17:58

결정트리 실습 리뷰

- 모델링에서 학습용, 평가용 데이터 분리 시 검증용 데이터까지 필요하다면 x_val, y_val 로 변수명 설정!

- max_depth의 기본값 = None

- 결정트리에서 변수 중요도를 표시: 트리 구조에서 특정 변수가 줄여준 총 불순도의 양이 많은 순서 (전체에서 차지한 비율)

**max_depth를 주면 변수 중요도가 달라짐! Why? 트리의 깊이(단계)가 줄어들기 때문에 당연히 변수 중요도가 달라짐

CH4. Logistic Regression(로지스틱 회귀분석)

확률문제를 선형회귀로 모델링, 로지스틱 회귀

공부 시간에 따라 합격 (1) 불합격 (0)으로 나눔!
범주값도 숫자이기 때문에 선형 회귀모델을 만들 수는 있음!
그러나 아래의 그래프는 0,1 제외 다른값도 존재! 결과는 0보다 작은값이나 1보다 큰 값은 없기 때문에 문제가 발생함!

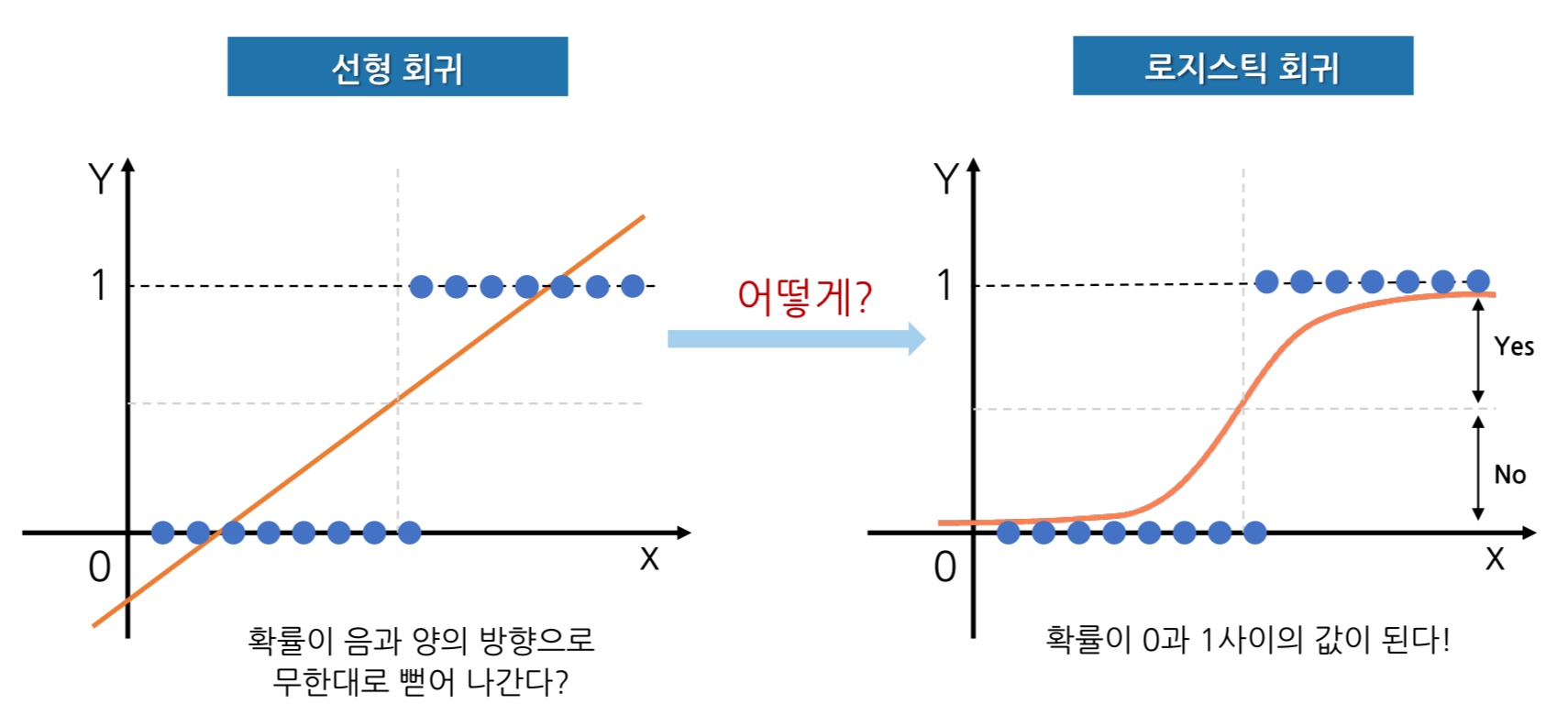
→ 이를 개선하기 위해 0.5보다 크면 1, 0.5보다 작으면 0으로 판단하는 식으로 분류 문제에 활용할 수 있다고 판단!

→ 임계값(0.5)을 조절하면서 분류 문제 판단을 적극적 or 소극적으로 구분할 수 있음

**0.45로 임계값을 설정 시 더 적극적으로 1로 판단!

로지스틱 함수

시그모이드(sigmoid) 함수라고도 부름
확률 값 p는 선형 판별식값이 커지면 1, 작아지면 0에 가까워짐!
(-∞, ∞) 범위를 갖는 선형 판별식 결과로 (0, 1) 범위의 확률 값을 얻음!
- (0, 1) : 소괄호로 범위 표현하면 0, 1은 포함되지 않는 범위
- [0, 1] : 대괄호로 범위 표현하면 0, 1도 포함된 범위
기본적으로 확률 값 0.5를 임계값으로 가지고 있음! (임계값 바꾸려면 수동으로 만들어야 함!)

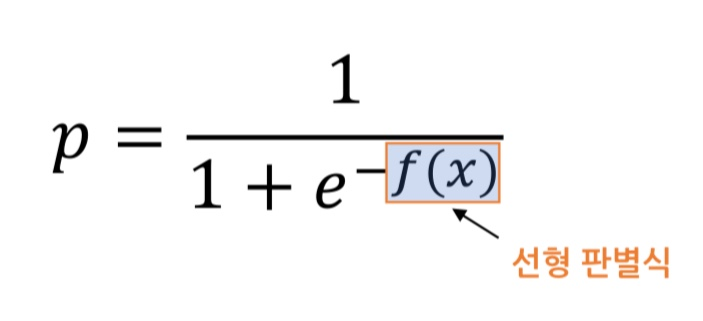
모델링

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, classification_report   # 성능평가 주의
model = LogisticRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

임계값 조정

# 예측값 확인
y_pred[10:20]

# 예측 확률: x_test가 0이될 확률, 1이될 확률을 보여줘!
# 오른쪽이 0.5보다 크면 1로 예측
p = model.predict_proba(x_test)
p[10:20]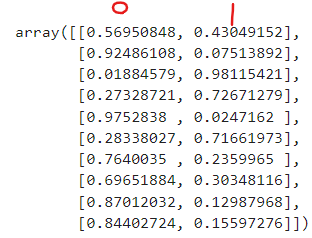

# 임계값을 0.45로 생각해서 수동 분류
p1 = p[:, [1]]

# 1로 분류될 확률값 확인 (오른쪽 열만 가져오기)
p1[10:20]

# 임계값: 0.5, 반복문 확장 # 여기서 나온 결과값은 y_pred 값과 같음
y_pred2 = [1 if x > 0.5 else 0 for x in p1] # 0.5보다 크면 1, 아니면 0
y_pred2[10:20]

# 성능 평가
print(classification_report(y_test, y_pred2))

- 임계값을 0.45로 설정하면서 적극적으로 분류하면 precision을 떨어뜨리더라도 recall을 올릴 수 있음!

- 변수가 많을 때 복잡해짐 !! multi class 도 분류 가능!

- 회귀식을 세 개를 만들기! (A, B, C), 각각의 확률 값을 얻어서 가장 큰 확률값을 가진 것으로 설정

1) A = 1, B/C = 0

2) B = 1, A/C = 0

3) C = 1, B/C = 0

- 회귀식을 하나로 만들어서, soft max함수를 사용해 확률값으로 바꿔주는 방법도 있음!

- # 2단계: 선언하기에서 multi_class = 'ovr'로 설정하면 다중 분류를 이진 분류로 만듦
model = LogisticRegression(multi_class='ovr')

K-Fold Cross Validation

Random Split의 문제

새로운 데이터에 대한 모델의 성능을 예측하지 못한 상태에서 최종 평가를 수행
무작위로 분할하면 여러 번 학습시켜도 같은 데이터 셋으로만 성능 평가 하는 것임!

K-분할 교차 검증 개념

모든 데이터가 평가에 한 번, 학습에 k-1번 사용되어 여러 번 검증해 성능을 예측하는 것!
k개의 분할 (k>=2)에 대한 성능을 예측해서 일반화 성능을 구하는 것 (디폴트 k=5)
최종 정확도 = Average(Round1, Round2, Round3..., Round10)
튜닝 전 우리 모델의 성능이 어떤 지 예측해보는 것!
- 장점: 가지고 있는 데이터를 최대한 효율적으로 활용해 과소적합을 방지할 수 있음, 일반화된 모델 만들 수 있음
- 단점: 반복 횟수가 많아서 학습, 평가에 많은 시간 소요!

성능 예측

- k 분할 교차 검증 방법으로 모델의 성능을 예측

- cross_val_score(model, x_train, y_train, cv=n) 형태로 사용! cv는 k값의 개수 지정 (분할 개수, 기본값=5)

- cross_val_score 함수는 넘파이 배열 형태의 값을 반환 / cross_val_score 함수 반환 값의 평균이 예측 성능!

1) Decision Tree(결정트리)

# 불러오기
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score

# 선언하기
model = DecisionTreeClassifier(random_state=1)

# 검증하기 (학습 데이터 전달, 정확도에 대한 성능, 만약 회귀라면 r2)
cv_score = cross_val_score(model, x_train, y_train, cv=10)

# 확인
print(cv_score)
print('평균:', cv_score.mean())
print('표준편차:', cv_score.std())

# 예측 결과 저장
result = {}
result['Decision Tree'] = cv_score.mean()

# 확인
result

- 결정트리와 KNN, 로지스틱 회귀분석 각 예측 성능 비교를 위해 딕셔너리에 추가~

2) KNN

# 불러오기
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score

# 선언하기
model = KNeighborsClassifier()

# 검증하기
cv_score = cross_val_score(model, x_train, y_train, cv=10)

# 확인
print(cv_score)
print(cv_score.mean())

# 예측 결과 저장
result['KNN'] = cv_score.mean()

# 확인
result

3) Logistic Regression

# 불러오기
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score

# 선언하기
model = LogisticRegression()

# 검증하기
cv_score = cross_val_score(model, x_train, y_train, cv=10)

# 확인
print(cv_score)
print(cv_score.mean())

# 예측 결과 저장
result['Logistic Regression'] = cv_score.mean()

# 확인
result

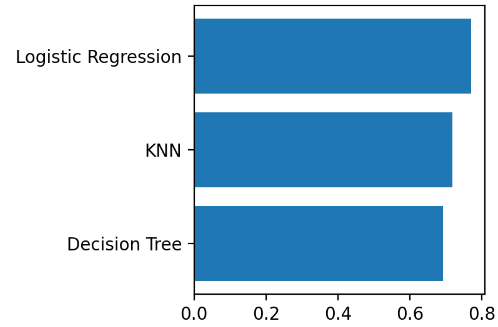
- 세 가지 중에는 Logistic Regression이 가장 좋은 성능으로 예측됨!

- 그러나 의사결정트리는 max_depth 설정하고, KNN은 변수 제거를 하면 다른 결과가 나올 수도 있음!

** 위의 코딩은 단지 성능을 예측하는 것이므로 정식 학습이 필요함!

** k-분할은 성능 예측이라는 점을 꼭 기억!!

4) 성능 시각화 비교

plt.figure(figsize=(3,3))
#plt.barh(y=list(result.keys()), width=result.values())
plt.barh(y=list(result), width=result.values())
plt.show()

Hyperparameter 튜닝

CH1. Hyperparameter

모델의 성능 향상을 위해 최선의 하이퍼파라미터값을 찾는 것! (Grid Search, Random Search 등)

KNN

k 값에 따라 성능이 달라짐 → k 값이 가장 클 때 (=전체 데이터 개수) 가장 단순한 모델인 평균, 최빈값이 됨
k 값이 작을수록 복잡한 모델 ! (과적합 가능성 올라감)
거리 계산법에 따라 성능이 달라질 수 있음! (유클리드 거리, 맨하튼 거리)

Decision Tree

max_depth: 트리의 최대 깊이 제한, 기본값(None)으로 데이터 개수가 min_samples_split보다 작아질 때까지 계속 깊이를 증가시킴 → 값이 작을수록 트리 깊이가 제한되어 모델이 단순해짐!
min_samples_leaf: leaf가 되기 위한 최소한의 샘플 데이터 수, 기본값은 1→ 값이 클수록 모델이 단순해짐!
min_samples_split: 노드를 분할하기 위한 최소한의 샘플 데이터 수, 기본값은 2 → 값이 클수록 모델이 단순해짐!

CH2. Random Search, Grid Search

KNN 알고리즘: 이웃 개수인 k값을 어떻게 설정하는가에 따라 모델 성능이 달라짐

1) 방법1 : Grid Search

① 1~n 구간의 정수를 n_neighbors 값으로 해서 모델 성능 정보 수집 (파라미터 값 범위를 모두 사용)

② 가장 성능이 좋았던 때의 n_neighbors 값을 찾음

③ 이 값을 갖는 KNN 모델 선언 !

** n이 크면 상당히 많은 시간이 소요! but 전부 test했기 때문에 아쉬움이 없음

2) 방법2 : Random Search

① 1~n 구간의 정수 중 무작위로 m개를 골라 n_neighbors 값을 찾음 (파라미터 값 범위에서 몇 개 선택할지 지정)

② 가장 성능이 좋았던 때의 n_neighbors 값을 찾음

③ 이 값을 갖는 KNN 모델 선언 !

** 임의의 m개를 골랐기 때문에 시간 소모 적음 , but 더 좋은 성능을 보이는 값이 있을 가능성이 있음 ㅠㅠ

- Grid Search, Random Search를 사용할 때 내부적인 K-Fold Cross Validation을 위해 cv 값 지정

→ 실제 수행되는 횟수는 파라미터 조합 수 x cv 값

Random Search + Grid Search 적용 고려

하이퍼파라미터 값을 어떻게 정해야 할 지 모르겠을 때
- Random Search와 Grid Search를 함께 사용할 수 있음
- Random Search로 먼저 범위 지정 후 무작위 수행 n_iter값 지정해서 최적값 판단
- 그 후 Grid Search로 근처에 있는 값들 중 더 괜찮은 값이 있을지 확인!

Hyperparameter 튜닝 시 주의사항

파라미터 조정으로 최적화된 성능 얻었다고 해도, 운영환경(평가 데이터)에서의 성능이 보장 되지는 않음!
- 과적합, 미래 발생할 데이터 과거와 다를 수 있음!

** stratify는 주로 분류 문제에서 학습 데이터와 평가 데이터가 같은 수로 나눠지기 위한 것임! (시계열이나 회귀에서는 사용 안 함)

모델 튜닝

1) RandomizedSearchCV 알고리즘 사용하는 모델 선언

- 기본 모델 이름, 파라미터 변수, cv(k-fold 분할 개수, default=5), n_iter(시도 횟수, default=10), scoring(평가 방법)

# 불러오기
from sklearn.model_selection import RandomizedSearchCV
# 파라미터 선언
  # max_depth: 1~50
param = {'max_depth': range(1, 51)}

# Random Search 선언
  # cv=5
  # n_iter=20
  # scoring='r2'
model = RandomizedSearchCV(model_dt,    # 튜닝할 기본 모델
                          param,        # 테스트 대상 매개변수 범위
                          n_iter=20,    # 임의로 선택할 매개변수 개수
                          cv=5,         # K-Fold cv 개수
                          scoring='r2') # 사용할 평가지표 → 보통 r2
# 학습하기
model.fit(x_train, y_train)

2) 결과 확인

- model.cv_results_['mean_test_score']: 테스트로 얻은 성능

- model.best_params_: 최적의 파라미터

- model.best_score_: 최고의 성능

# 중요 정보 확인
print('=' * 80)
print(model.cv_results_['mean_test_score'])
print('-' * 80)
print('최적파라미터:', model.best_params_)
print('-' * 80)
print('최고성능:', model.best_score_)
print('=' * 80)

** 의사결정트리에서는 최적 파라미터값 max_depth가 보통 3~7 사이로 나옴!

3) 변수 중요도

# 변수 중요도, width=model.best_estimator_까지 써야 결정트리가 됨!
plt.figure(figsize=(5, 5))
plt.barh(y=list(x), width=model.best_estimator_.feature_importances_)
plt.show()

- 그리드 서치, 랜덤 서치는 feature_importances_ 속성이 없음!

→ 변수 중요도를 확인하려면 best_estimator_써줘야 함!